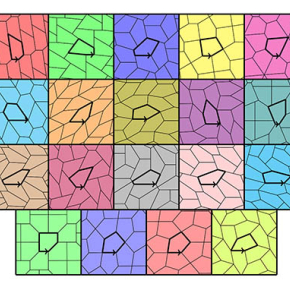
Il n'existe que 15 pavages pentagonaux possibles
Recouvrir une surface plane avec un motif unique est un problème mathématique qui intéresse l'Homme depuis l'Antiquité, notamment pour la qualité esthétique des pavages, comme les mosaïques et les carrelages. L'un des problèmes encore ouvert dans ce domaine, qui questionne la communauté scientifique depuis 1918, est aujourd'hui définitivement clos grâce à Michaël Rao du Laboratoire d'informatique du parallélisme (CNRS/Inria/ENS de Lyon/Université Claude Bernard Lyon 1) : en utilisant des outils informatiques, il a démontré que pour des motifs à cinq côtés, seules 15 formes sont possibles pour recouvrir une surface plane. Ces travaux sont aujourd'hui disponibles sur le site Arxiv.org.
Pour recouvrir un sol avec une seule et même forme, il existe de nombreuses solutions : triangles, carrés, rectangles, hexagones, etc. La recherche exhaustive de toutes les formes convexes pouvant paver un plan, c'est-à-dire une forme avec des angles inférieurs à 180° et qui permettent de recouvrir tout un mur sans chevauchement, fut initiée par Karl Reinhardt durant sa thèse en 1918. Il a montré que tous les triangles et quadrilatères pavent le plan, qu'il n'existe que 3 types d'hexagones qui permettent de réaliser un pavage et qu'un polygone à sept côtés ou plus ne permet pas de recouvrir un plan. Seule la question des pentagones restait ouverte.
De 1918 à 2015, 15 types de pentagones ont été découverts, lors de recherches plutôt singulières : initiée par Reinhardt en 1918, elle a subi plusieurs rebondissements, comme des nouvelles découvertes de mathématiciens amateurs, jusqu'à l'annonce médiatisée, en 2015, d'une nouvelle et 15e forme, 30 ans après la 14e, sans que la communauté scientifique ne parvienne à déterminer s'il existait encore d'autres formes de pentagones possibles pour paver un plan.
Michaël Rao, chercheur du CNRS au Laboratoire d'informatique du parallélisme (CNRS/Inria/ENS Lyon/Université Claude Bernard Lyon 1) a aujourd'hui définitivement montré qu'il n'existe qu'un ensemble fini de familles 1
de pentagones à considérer. En générant toutes les possibilités via un programme informatique 2
, Michaël Rao a montré que 371 familles de pentagones pouvaient potentiellement recouvrir un plan. Il a ensuite testé chacune de ces familles, à l'aide d'un autre programme informatique, et a montré que seuls 19 types de pentagones satisfaisaient les conditions nécessaires, à la fois pour les angles et la longueur des côtés, pour paver un plan. Parmi ces 19 types, 15 correspondent à des types déjà connus, et les quatre autres s'avèrent être des cas particuliers de ces 15 types. Seuls 15 types de tuiles sont donc possibles pour un recouvrir une surface plane.
Avec sa méthodologie, Michael Rao clôt ainsi un problème vieux d'un siècle, mais pas seulement. Toutes les tuiles convexes pavent le plan de façon périodique (c'est-à-dire que le pavage se répète à l'infini). On ne sait pas encore s'il existe une tuile qui permet de réaliser un pavage non-périodique. Or, la plupart des techniques utilisées ici peuvent également être utilisées dans le cas des polygones non convexes et pourraient donc servir de base à la résolution de cet autre problème encore ouvert dans le domaine des pavages, plus connu sous le nom d' "Einstein Problem" (de l'allemand "ein stein").
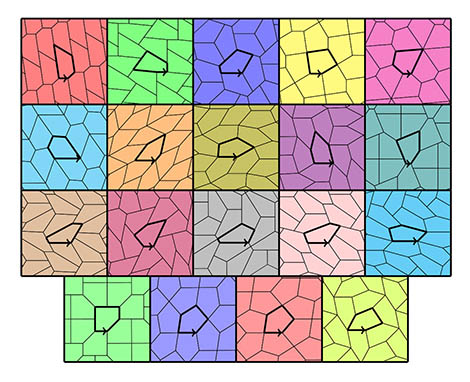
(CNRS/Inria/ENS de Lyon/Université Claude Bernard Lyon 1).
Les 15 types de pavages pentagonaux et leurs 4 types particuliers.
Exhaustive search of convex pentagons which tile the plane. Michaël Rao, disponible sur Arxiv.org, arXiv:1708.00274 (Consulter le site web)