Derrière le phénomène des « eaux-mortes »

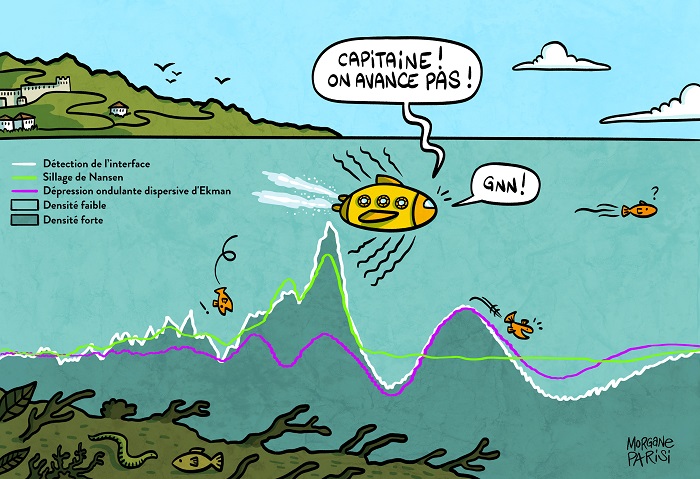
En 1893, l'explorateur norvégien Fridtjof Nansen fut le témoin d'un étrange phénomène alors qu’il naviguait au nord de la Sibérie : son bateau fut freiné par une force mystérieuse et il eut beau faire des tours et des détours, il ne retrouva pas sa vitesse normale. En 1904, l’océanographe et physicien suédois Vagn Walfrid Ekman a montré, en laboratoire, que des vagues, formées sous la surface, à l’interface entre la couche d’eau salée et la couche d’eau douce constituant la partie supérieure de cette zone de l’océan arctique, interagissaient avec le bateau, jusqu’à le freiner.

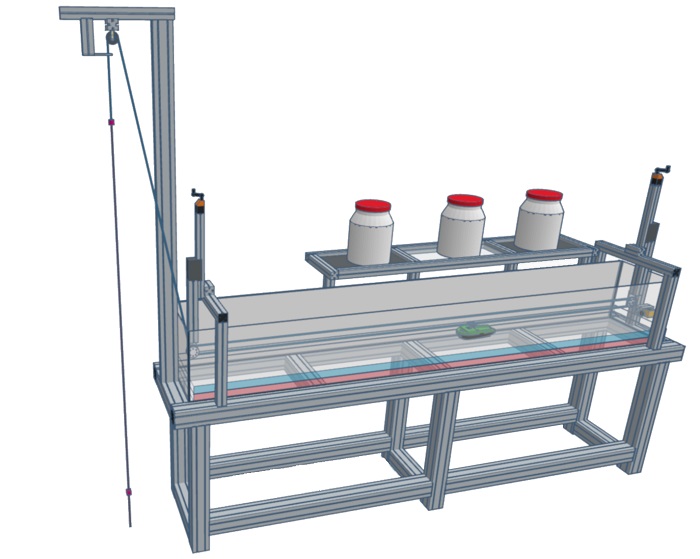
Ce phénomène, dit d’ « eaux mortes », peut s’observer dans toutes les mers et océans où se mélangent des eaux de différentes densités (à cause de la salinité ou de la température). Il désigne deux phénomènes de résistance observés par les scientifiques. Le premier, le « phénomène de résistance d'ondes internes à la Nansen », amène à une vitesse constante, même si anormalement basse, du bateau. Le second, le « phénomène de résistance d'ondes internes à la Ekman », est caractérisé par des oscillations de la vitesse du bateau piégé, dont l'origine restait obscure. Des physiciens, des mécaniciens des fluides et des mathématiciens de l’Institut Pprime du CNRS et du Laboratoire de mathématiques et applications (CNRS/Université de Poitiers) ont tenté à leur tour de résoudre ce mystère, notamment grâce à une classification mathématique de différentes ondes internes et une analyse des images expérimentales sous l'échelle du pixel, une première.

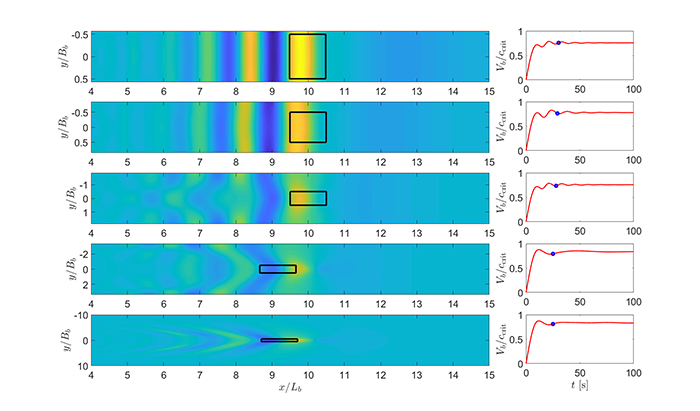
Ils ont ainsi montré que ces variations de vitesse sont dues à la génération d’ondes spécifiques qui agissent comme un tapis roulant bosselé sur lequel le navire se déplace d'avant en arrière. Les scientifiques ont de plus réconcilié les deux observations de Nansen et Ekman. Ils ont montré que le régime oscillant d’Ekman n'est que temporaire : le navire finit par s’en échapper, pour atteindre la vitesse constante de Nansen.

Ces travaux s’inscrivent dans un vaste projet1 cherchant à comprendre pourquoi, lors de la bataille d’Actium (31 avant J.-C.) les gros bateaux de Cléopâtre ont perdu face aux frêles navires d’Octave. La baie d’Actium, qui présente toutes les caractéristiques d’un fjord, aurait-elle pu piéger les bateaux de la reine d’Egypte dans des eaux-mortes ? Une autre hypothèse à envisager pour expliquer cette défaite retentissante, que l’on attribuait dans l’antiquité aux rémoras, des « poissons-ventouses » collés à leur coque, comme le veut une légende.

• 1Ces travaux ont été financés par l’appel à projets interdisciplinaire 80|Prime 2019 (projet OFHYS) et par la Mission pour les initiatives transverses et interdisciplinaires du CNRS.